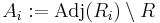Cuthill–McKee algorithm
In the mathematical subfield of matrix theory, the Cuthill–McKee algorithm (named for Elizabeth Cuthill and J. McKee) [1] is an algorithm to permute a sparse matrix that has a symmetric sparsity pattern into a band matrix form with a small bandwidth. The reverse Cuthill–McKee algorithm (RCM) due to Alan George is the same algorithm but with the resulting index numbers reversed. In practice this generally results in less fill-in than the CM ordering when Gaussian elimination is applied.[2]
The Cuthill McKee algorithm is a variant of the standard breadth-first search algorithm used in graph algorithms. It starts with a peripheral node and then generates levels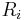 
for 
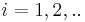until all nodes are exhausted. The set 
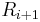is created from set 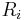by listing all vertices adjacent to all nodes in 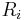. These nodes are listed in increasing degree. This last detail is the only difference with the breadth-first search algorithm.
Algorithm
Given a symmetric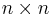 
matrix we visualize the matrix as the adjacency matrix of a graph. The Cuthill–McKee algorithm is then a relabeling of the vertices of the graph to reduce the bandwidth of the adjacency matrix.
The algorithm produces an ordered n-tuple R of vertices which is the new order of the vertices.
First we choose a peripheral vertex x and set R := ({x}).
Then for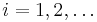 
we iterate the following steps while |R| < n
- Construct the adjacency set
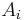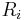of (with 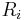the i-th component of R) and exclude the vertices we already have in R
- Sort 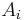with ascending vertex order.
- Append 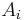to the Result set R.
In other words, number the vertices according to a particular breadth-first traversal where neighboring vertices are visited in order from lowest to highest vertex order.
See also
References
- ^ E. Cuthill and J. McKee. Reducing the bandwidth of sparse symmetric matrices In Proc. 24th Nat. Conf. ACM, pages 157–172, 1969.
- ^ J. A. George and J. W-H. Liu, Computer Solution of Large Sparse Positive Definite Systems, Prentice-Hall, 1981